前面對影響加工精度的各種主要因素進行了討論,從分析方法上來講,這是屬于局部的、單因素的。而實際生產中影響加工精度是多因素的、是錯綜復雜的。用單因素估算法去分析因果關系是難以說明的。為此,生產中常采用統計分析法,通過對一批工件進行檢查測量,將所測得的數據進行處理與分析,找出誤差分布與變化的規律,從而找出解決問題的途徑。
一、 加工誤差的分類
加工誤差按其性質的不同,可分為系統誤差和隨機誤差(也稱偶然誤差)。
1、 系統誤差: 包括常值系統誤差和變值系統誤差 。
(1) 常值系統誤差:
定義:在連續加工一批工件中,其加工誤差的大小和方向都保持不變或基本不變的系統誤差,稱為常值系統誤差。
例如:原理誤差,機床、刀具、夾具、量具的制造誤差,工藝系統靜力變形等原始誤差,都屬于常值系統誤差。如鉸刀的直徑偏大0.02mm,加工后一批孔的尺寸也都偏大0.02mm。
特點:
①與加工(順序)時間無關;
②預先可以估計;
③較易完全消除;
④不會引起工件尺寸波動(常值系統誤差對于同批工件的影響是一致的,不會引起各工件之間的差異);
⑤不影響尺寸分布曲線形狀。
(2) 變值系統誤差:
定義:在連續加工一批工件中,其加工誤差的大小和方向按一定規律變化的系統誤差,稱為變值系統誤差。
例如:刀具的正常磨損引起的加工誤差,其大小隨加工時間而有規律地變化,屬于變值系統誤差。
特點:
①與加工(順序)時間有關;
②預先可以估計;
③較難完全消除;
④會造成工件尺寸的增大或減小(變值系統誤差雖然會引起同批工件之間的差異,但是按照一定的規律而依次變化的,不會造成忽大忽小的波動);
⑤影響尺寸分布曲線形狀。
注意1:工藝系統的熱變形,在溫升過程中,一般將引起變值系統誤差,在達到熱平衡后,則又引起常值系統誤差。
2、 隨機誤差:
定義:在連續加工一批工件中,其加工誤差的大小和方向是無規則地變化著的,這樣的誤差稱為隨機誤差。
例如:毛坯誤差(加工余量不均勻,材料硬度不均勻等)的復映、定位誤差、夾緊誤差(夾緊力時大時小)、工件內應力等因素都是變化不定的,都是引起隨機誤差的原因。
特點:
①預先不能估計到;
②較難完全消除,只能減小到最小限度;
③工件尺寸忽大忽小,造成一批工件的尺寸分散(在一定的加工條件下隨機誤差的數值總在一定范圍內波動)。
注意2:隨機誤差和系統誤差的劃分也不是絕對的,它們之間既有區別又有聯系。
例如:加工一批零件時,如果是在機床一次調整中完成的,則機床的調整誤差引起常值系統誤差;如果是經過若干次調整完成的,則調整誤差就引起隨機誤差了。
注意3:誤差性質不同,解決的途徑也不同。
對于常值系統誤差誤差,若能掌握其大小和方向。就可以通過調整消除;對于變值系統誤差,若能掌握其大小和方向隨時間變化的規律,則可通過自動補償消除;惟對隨機誤差,只能縮小它們的變動范圍,而不可能完全消除。
二、 加工誤差的統計分析
常用的統計分析法有兩種:分布曲線法和點圖法。
(一) 分布曲線法
1、 實際分布曲線(直方圖):
1)樣本和樣本容量:
樣本:采用調整法成批加工某種零件,隨機抽取其中一定數量(50~100)進行測量,抽取的這批零件稱為樣本。
樣本容量:樣本的件數稱為樣本容量。用n表示。
2)尺寸分散與尺寸分散范圍:
由于隨機誤差和變值系統誤差的存在,這些零件加工尺寸的實際數值是各不相同的,這種現象稱為尺寸分散。
樣本尺寸的最大值Xmax與最小值Xmin之差,稱為尺寸分散范圍。
3)分組及組距d: 將樣本尺寸按大小順序排列,分成k組,則組距d為:d=(Xmax-Xmin)/k, 分組數k的選定表如下:
| 樣本容量n | 50以下 | 50~100 | 100~250 | 250以上 |
| 分組數k | 6~7 | 6~10 | 7~12 | 10~20 |
4)頻數m:同一尺寸間隔的零件數量,稱為頻數,用m表示。
5)頻率f:頻數m與樣本容量n之比,稱為頻率。用f表示。 即:f=m/n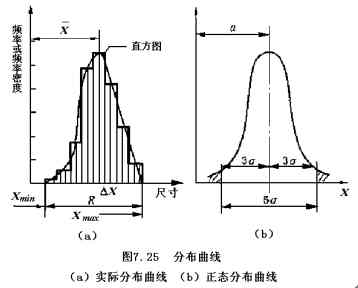
6)實際分布曲線(直方圖): 以工件尺寸(或誤差)為橫坐標,以頻數或頻率作縱坐標,即可作出該批零件加工尺寸的等寬直方圖。再連接直方圖中每一直方寬度的中點(組中值)得到一條折線,即實際分布曲線,見上圖(a)。
2、 正態分布曲線: 實踐和理論分析表明,當用調整法加工一批總數極多的而且這些誤差因素中又都沒有任何優勢的傾向時,其分布服從正態分布曲線(又稱高斯曲線),見上圖(b)。
(1)正態分布的曲線方程: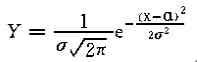
式中 Y——正態分布的概率密度;
α——正態分布曲線的均值;
σ——正態分布曲線的標準偏差(均方根偏差)
理論上的正態分布曲線是向兩邊無限延伸的,而在實際生產中產品的尺寸值卻是有限的。因此用有限的樣本平均值X和樣本標準偏差S作為理論均值α和標準偏差σ的估計值。其計算公式如下: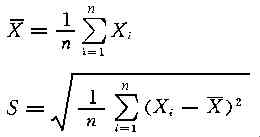
式中 X——工件的尺寸;
X——樣本平均值,即工件的平均尺寸;
Xi——第i個工件的尺寸;
S——樣本標準偏差,其值表示工件尺寸的分散程度;
n---樣本容量。
(2)正態分布曲線的特點:
1)均值α:決定正態分布曲線的中心位置,且在其左右對稱: 當X=α時,是曲線Y的最大值,即: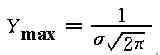
2)標準偏差σ是決定曲線形狀的參數: σ值增大,則Ymax減小,曲線將趨于平坦,尺寸分散性越大;相反,σ值越小,則曲線瘦高,尺寸分散性越小。故σ值表明了一批工件加工精度的高低(σ值小,Ymax值大,加工精度高)。σ的大小完全由隨機誤差所決定。
3)正態分布曲線與橫坐標軸沒有交點,即Y≠0: 說明工件尺寸分散有一定范圍。
4)分布曲線下所包含的全部面積代表一批加工零件,即100%零件的實際尺寸都在這一分布范圍內。對于正態分布曲線來說,由α到X曲線下的面積由下式決定:
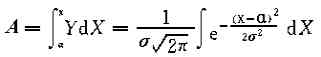
當X-α=3σ時,則:2A=0.9973=99.73%,即工件尺寸在±3σ以外的頻率只占0.27%,可以忽略不計。因此,一般都取正態分布曲線的分散范圍為土3σ。
正態分布曲線下的面積函數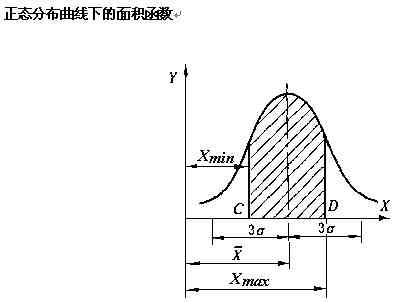
利用正態分布曲線計算產品合格率
3、 分布曲線的應用
1) 判別加工誤差的性質: 假如加工過程中沒有△變,那么其尺寸分布應服從正態分布,這是判別加工誤差性質的基本方法。
Ⅰ)實際分布曲線與正態分布曲線基本相符,說明加工過程中沒有△變;
Ⅱ)根據平均值X是否與公差帶中心重合,來判斷是否存在△常:平均值X與公差帶中心重合,說明不存在△常;平均值X與公差帶中心不重合,說明存在△常。
Ⅲ)△常僅影響平均值X,即只影響分布曲線的位置。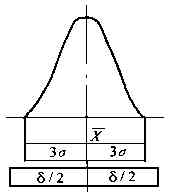
符合正態分布;δ≥6σ;且尺寸分布中心與公差帶中心重合。
說明:加工條件正常、△系幾乎不存在,△隨小,加工過程中無廢品出現,工序精度滿足要求。
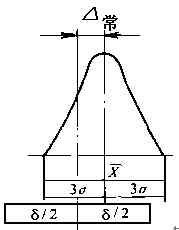
符合正態分布;δ≥6σ;但尺寸分布中心與公差帶中心不重合,存在△常。
說明:△變幾乎不存在,△隨小,有突出的△常存在。它主要是由于刀具安裝調整不準而造成的。在這種情況下,即使出現了廢品也是可以通過調整加以避免的(調整刀具起始加工位置,消除△常)。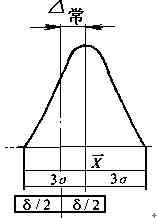
符合正態分布,δ<6σ,且尺寸分布中心與公差帶中心不重合。
說明:△變幾乎不存在,存在突出的△常,△隨較大。即使通過刀具調整消除了△常,也不能完全避免廢品的產生。工序精度不能滿足工件加工精度的要求。應換用一種比現用工序更精確的加工方法來完成加工(即減小工序σ值)。例如將車削加工換成磨削加工,將擴孔加工換成鉸孔等。
Ⅳ) 實際分布曲線不符合正態分布時,如出現的分布曲線呈平頂分布、雙峰分布或偏態分布時,說明加工過程中有突出的△變存在。
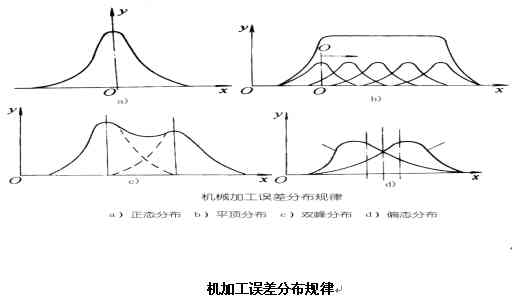
| 平頂分布 | 在影響機械加工中的諸多誤差因素中,如果刀具線性磨損的影響顯著,則工件的尺寸誤差將呈現平頂分布。平頂誤差分布曲線可以看成是隨時間而平移的眾多正態誤差分布曲線組合的結果。 |
| 雙峰分布 | 同一工序的加工內容中,由兩臺機床來同時完成,由于這兩臺機床的調整尺寸不盡相同,兩臺機床的精度狀態也有差異,若將這兩臺機床所加工的工件混在一起,則工件的尺寸誤差就呈雙峰分布。 |
| 偏態分布 | 在用試切法車削軸徑或孔徑時,由于操作者為了盡量避免產生不可修復的廢品,主觀地(而不是隨機地)使軸頸加工得寧大勿小,則它們得尺寸誤差就呈偏態分布。 |
機加工誤差分布規律
平頂分布 在影響機械加工中的諸多誤差因素中,如果刀具線性磨損的影響顯著,則工件的尺寸誤差將呈現平頂分布。平頂誤差分布曲線可以看成是隨時間而平移的眾多正態誤差分布曲線組合的結果。
雙峰分布 同一工序的加工內容中,由兩臺機床來同時完成,由于這兩臺機床的調整尺寸不盡相同,兩臺機床的精度狀態也有差異,若將這兩臺機床所加工的工件混在一起,則工件的尺寸誤差就呈雙峰分布。
偏態分布 在用試切法車削軸徑或孔徑時,由于操作者為了盡量避免產生不可修復的廢品,主觀地(而不是隨機地)使軸頸加工得寧大勿小,則它們得尺寸誤差就呈偏態分布。
2) 確定工藝能力及其等級
Ⅰ)工藝能力:是指工序處于穩定狀態時,加工誤差正常波動的幅度。 例如:加工尺寸服從正態分布時,其尺寸分散范圍應是6σ,所以工藝能力就是6σ。
Ⅱ)工藝能力等級:以工藝能力系數Cp來表示,Cp代表了工藝能滿足加工精度的程度。
其值按下式計算:Cp =δ/6σ
式中:δ---為工件尺寸公差。 根據工藝能力系數的大小,將工藝能力分成5級,其值見教材P209。
注:一般情況下,工藝能力不應低于二級。
3) 估算合格率或不合格率:
Q廢=0.5-A
(二)工藝過程的點圖分析
應用分布圖分析工藝過程精度的前提時工藝過程必須是穩定的。由于點圖分析法能夠反映質量指標隨時間變化的情況,因此,它是進行統計質量控制的有效方法。這種方法既可以用于穩定的工藝過程,也可以用于不穩定的工藝過程。
對于一個不穩定的工藝過程來說,要解決的問題是如何在工藝過程的進行中,不斷地進行質量指標的主動控制,工藝過程一旦出現被加工工件的質量指標有超出所規定的不合格品率的趨向時,能夠及時 調整工藝系統或采取其它工藝措施,使工藝過程得以繼續進行。對于一個穩定得工藝過程,也應該進行質量指標得主動控制,使穩定得工藝過程一旦出現不穩定趨勢時,能夠及時發現并采取相應得措施,使工藝過程繼續穩定地進行下去。
點圖分析法所采用的樣本使順序小樣本,即每隔一定時間抽取樣本容量n=5~10的一個小樣本,計算出各小樣本的算術平均值和極差R。 點圖使控制工藝過程質量指標分布中心的變化的,R點圖是控制工藝過程質量指標分散范圍的變化的,因此,這兩個點圖必須聯合使用,才能控制整個工藝過程
第四節 提高加工精度的途徑
減小加工誤差的方法主要有兩種:誤差預防和誤差補償。( 減小原始誤差、轉移原始誤差、均分原始誤差、均化原始誤差以及誤差補償。)
一、 誤差預防技術:
1、 直接減小原始誤差法: 主要是在查明影響加工精度的主要原始誤差因素之后,設法對其直接進行消除或減小的方法。
例如:加工細長軸時,主要原始誤差因素是工件剛性差,因而,采用反向進給切削法,并加跟刀架,使工件受拉伸,從而達到減小變形的目的。 (見P211圖7.32)
2、 轉移原始誤差法: 是把影響加工精度的原始誤差轉移到不影響或少影響加工精度的方向上。 例如:車床的誤差敏感方向是工件的直徑方向,所以,轉塔車床在生產中都采用"立刀"安裝法,把刀刃的切削基面放在垂直平面內,這樣可把刀架的轉位誤差轉移到誤差不敏感的切線方向。
3、 均分原始誤差法: 采用分組調整,把誤差均分:即把工件安誤差大小分組,若分成n組,則每組零件的誤差就縮小1/ n。
4、 “就地加工”法: 例如:車床尾架頂尖孔的軸線要求與主軸軸線重合,采用就地加工,把尾架裝配到機床上后進行最終精加工。又如六角車床轉塔上六個安裝刀架的大孔及端面的加工(見P212)。
二、 誤差補償技術:
1、 在線檢測: 加工中隨時測量工件的實際尺寸,隨時給刀具補償的方法。
2、 偶件自動配磨: 此法是將互配的一個零件作為基準,去控制另一個零件加工精度的方法。








 客服1
客服1 