刀具切削部分的幾何參數指刀具靜止參考系中確定的,刀具切削部分的前、后面和主、副切削刃空間位置的參數以及基于這些切削加工需要描述的幾何參數,其主要是各種幾何角度與刀面或切削刃的形狀等。如圖所示為基于典型的外圓車刀定義的幾何參數。
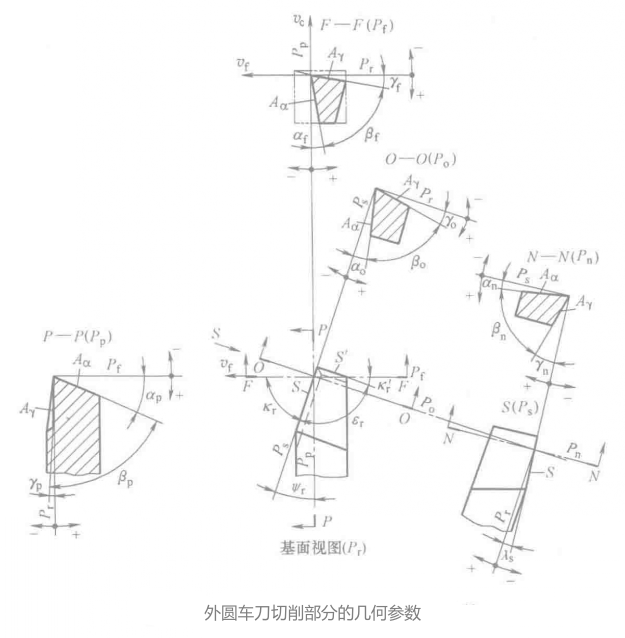
(1)基面Pr中測量的角度如下所述。
1)主偏角κr:在基面Pr中度量的,主切削平面Ps與假定工作平面Pf間的夾角。
2)副偏角κ'r:在基面Pr中度量的,副切削平面P's與假定工作平面Pf間的夾角。
3)余偏角φ:在基面Pr中度量的,主切削平面Ps與背平面Pp間的夾角。
4)刀尖角εr:在基面Pr中度量的,主切削平面Ps與副切削平面P's間的夾角。其是一個派生角度,與主偏角κr和副偏角κ'r的關系為:εr=180°-(κr+κ'r)。
(2)正交平面Po中測量的角度 如下所述,如圖中的O-O剖面,注意角度正負的判斷。
1)前角γo:在正交平面Po中度量的,前面Aγ與基面Pr間的夾角。當前面與切削平面夾角小于90°時,前角為正值;大于90°時,前角為負值。
2)后角αo:在正交平面Po中度量的,后面Aα與切削平面Ps間的夾角。當后面與基面夾角小于90°時,后角為正值;大于90°時,后角為負值,實際切削時一般不允許負后角。
3)楔角βo:在正交平面Po中度量的,前面Aγ與后面Aα間的夾角。其是一個派生角度,與前角γo和后角αo的關系為:βo=90°-(γo+ αo)。
(3)切削平面Ps中測量的角度上圖中的S向視圖,為刃傾角λs,其是切削平面Ps中度量的主切削刃S與基面Pr間的夾角。注意其用向視圖S進行表達。當刀尖相對安裝面處于最高點時,刃傾角為正值;反之,為負值;當刃傾角為零度時,切削刃在基面內。
依據以上定義,可以給出副切削刃上的副前角γ'o、副后角α'o和副刃傾角λ's的定義可自行分析,圖中未示出。
在上述角度中,前角γo和刃傾角λs確定前面Aγ ,的方位;主偏角,和后角確定主后面的Aα方位,此時,主切削刃S的方位也就自然確定。主切削刃S的方位也可認為是主偏角κr和刃傾角λs確定。由此可見,主切削刃及其前面和主后面在空間的方位只用四個基本角度 γo、αo、κr和λs就能完全確定。同理,用副前角 γ'o、副后角α'o、副偏角κ'r和副刃傾角λ's,則副切削刃S'及其對應的前面Aγ和副后面A'α在空間的方位也就完全確定。主切削刃S和副切削刃S'共處在前面Aγ中,其交點便是刀尖。由于前面Aγ是共用的,因此,副前角γ'o和副刃傾角λ's是可以計算出來的,即屬于派生角度。因此,外圓車刀切削部分的空間幾何結構僅需前角γo、后角αo、主偏角κr、副偏角κ'r、刃傾角λs以及負后角 α'o六個參數即可確定。
以上前角γo、后角αo和刃傾角λs允許出現負角,圖中正、負角度的判斷已有表示其規律是,以安裝面為基準,刀尖位置最高時為正角度,刀尖位置最低時則為負角度如圖中的刃傾角即為負值。
(4)法平面Pn中測量的角度 圖中的 N-N剖面,有法前角γn、法后角αn和法楔角βn。對于某些大刃傾角刀具,如立銑刀側切削刃,由于容屑槽的加工需要,常用到法平面參考系中測量的角度。同時,法楔角βn也直觀地表達出刀齒的強度。當λs=0°時,法平面與正交平面重合;當λs≠0°時,法平面與正交平面相夾λs。 1)法前角γn:在法平面Pn中度量的,前面Aγ與基面Pr間的夾角,有正、負之分。 2)法后角αn:在法平面Pn中度量的,后面Aα與切削平面Ps間的夾角,有正、負之分。
=0°時,法平面與正交平面重合;當λs≠0°時,法平面與正交平面相夾λs。
1)法前角γn:在法平面Pn中度量的,前面Aγ與基面Pr間的夾角,有正、負之分。
2)法后角αn:在法平面Pn中度量的,后面Aα與切削平面Ps間的夾角,有正、負之分。
3)法楔角βn:在法平面Pn中度量的,前面Aγ與后面Aα間的夾角。其是一個派生角度,即βn=90°-(γn+ αn)。
(5)在假定工作平面Pf和背平面Pp中測量的角度圖中的F-F剖面和P-P剖面,其在機械刃磨刀具以及分析討論切削問題等場合常用。在假定工作平面中測量的前角和后角分別稱為側前角γf和側后角αf,在背平面中測量的前角和后角分別稱為背前角γp和背后角 αp。
1)側前角γf:在假定工作平面Pf中度量的,前面Aγ與基面Pr間的夾角,有正、負之分。
2)側后角αf:在假定工作平面Pf中度量的,后面Aα與切削平面Ps間的夾角,有正、負之分。
3)側楔角βf:在假定工作平面Pf中度量的,前面Aγ與后面Aα間的夾角,βf=90°-(γf+αf)。
4)背前角γp:在背平面Pp中度量的,前面Aγ與基面Pr間的夾角,有正、負之分
5)背后角αp:在背平面Pp中度量的,后面Aα與切削平面Ps間的夾角,有正、負之分。
6)背楔角βp:在背平面 Pp中度量的,前面Aγ與后面Aα間的夾角,βp=90°-(γp+αp)。








 客服1
客服1 